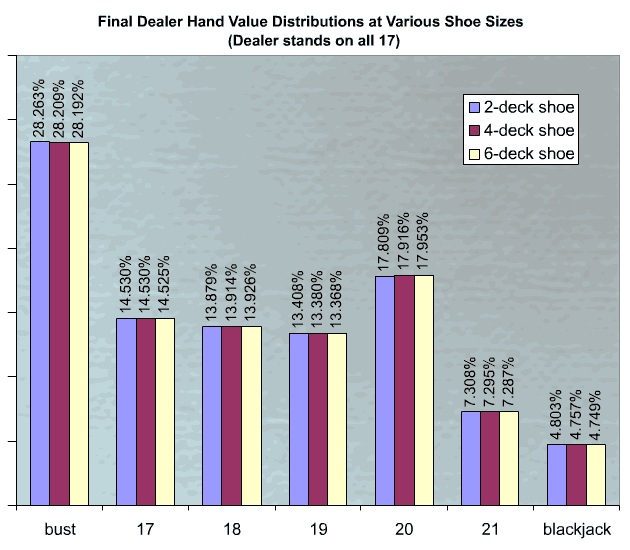
As you can see, the actual probabilities hardly change at all when adding more decks to the shoe. 20 becomes slightly more likely, mainly because the draw of a first 10-card (10/J/Q/K) is less of a drain on the probability of a second 10-card when so many more are in the deck.*

Similarly, the probability of bust decreases slightly. This is primarily because the draw of non-10-cards normally increases the probability of drawing a 10-card (and vice versa), but adding more decks lessens the effect.

It turns out dealer blackjack actually becomes less probable with the addition of more decks. The same principle applies. With a smaller deck, the draw of a non-ace lends a small but significant increase to the probability that the second card *will* be an ace. When the pool of cards increases, it diminishes the strength of this effect.

Take the two-deck (104 cards) case. The first card drawn is a ten. Given that all shuffles are equally probable, that as far as we know all eight aces remain in the deck, and that 103 cards are still unknown, the next card has an 8/103 chance of being an ace. This is slightly better odds than the 8/104 (1/13) chance of drawing an ace before we drew the ten.

In the six-deck case, there are 4 * 6 = 24 aces in the deck, and 52 * 6 = 312 cards in the deck. So the chances of drawing an ace are 24/312 (1/13) until we draw our ten, and the chances improve to 24/311. 8/103 is almost a full percentage point greater than 8/104, but 24/311 is only a third of a percent greater than 24/312.

The effect is compounded when you consider the other half of dealer blackjacks where the ace is dealt first.

In summary, the casino margins probably don't change significantly as a direct result of the probability shifts we see here. Adding more decks simply reduces visibility into the deck, reducing the benefits of card-counting and making effective card-counting strategies far more difficult to compute.

Detailed tables broken out by dealer's "up" card.

* Card counting strategies operate on this principle, ie, that the odds of receiving a specific card improve or decrease once you know something about the cards that have already been dealt. Take the following case: if several hands go by and no aces have been dealt, the proportion of cards left in the deck which are aces is much higher than normal. Thus, the chances that the next card will be an ace is better than it is typically. This information should affect your decisions to hit/double/stand/split if you wish to gain an advantage over the house.